Dari membangun piramida di Mesir kuno hingga navigasi menggunakan bintang oleh para pelaut kuno, tahukah kamu bahwa trigonometri telah menjadi alat vital dalam peradaban manusia? Yap, trigonometri bukan cuma tentang segitiga aja, Skollamate. Trigonometri memungkinan kita untuk mengukur berbagai hal dan memahami bentuk dan ruang, lho.
Kakmin yakin kamu bakal jatuh cinta sama trigonometri, deh. Tapi sebelum mempelajari kegunaan trigonometri lebih lanjut, yuk pelajari pengertian dan rumus trigonometri di bawah ini!
Pengertian dan Kegunaan Trigonometri
Kata trigonometri berasal dari bahasa Yunani, di mana trigonon berarti “tiga sudut” dan metron berarti “mengukur”.
Trigonometri merupakan cabang ilmu Matematika yang mempelajari hubungan antara sisi dan sudut dalam sebuah segitiga. Hubungan ini biasanya dinyatakan dalam bentuk perbandingan sinus, kosinus, dan tangen. Dengan menggunakan perbandingan ini, kamu dapat dengan mudah menentukan panjang sisi segitiga meskipun hanya mengetahui panjang satu sisi dan sudutnya saja.
Lalu, buat apa sih ilmu ini dipelajari?
Tentunya sebuah ilmu dipelajari untuk memudahkan aktivitas manusia. Kegunaan trigonometri sendiri sangat banyak, mulai dari bidang astronomi, teknik sipil, geografi, oseanografi, arsitektur, fisika, kesehatan, hingga waktu salat, dan masih banyak lagi.
Rumus Trigonometri Dasar
Rumus paling dasar dalam trigonometri melibatkan definisi fungsi-fungsi dasar trigonometri yang dinyatakan sebagai perbandingan sisi-sisi segitiga siku-siku, seperti di bawah ini.
- Sinus (sin)
sin α = panjang sisi depan/panjang sisi miring - Cosinus (cos)
cos α = panjang sisi samping/panjang sisi miring - Tangen (tan)
tan α = panjang sisi depan/panjang sisi samping - Kosekan (cosec)
csc α = 1/sin α= panjang sisi miring/panjang sisi depan - Sekan (sec)
sec α = 1/cos α= panjang sisi miring/panjang sisi samping - Kotangen (cot)
cot α = 1/tan α= panjang sisi samping/panjang sisi depan

Rumus-rumus ini mendasarkan pada definisi dasar trigonometri dalam konteks segitiga siku-siku, di mana α merupakan sudut dalam segitiga tersebut.
Identitas Trigonometri
Identitas trigonometri adalah suatu pernyataan matematis yang menunjukkan kesetaraan antara dua ekspresi trigonometri. Pada dasarnya, identitas ini memungkinkan kita untuk mengubah atau menjelaskan satu fungsi trigonometri di sisi kiri atau kanan persamaan sehingga menghasilkan bentuk akhir yang sama dengan sisi lainnya.
Contoh sederhana dari identitas trigonometri adalah tan α + cot α = sec α . csc α
Dalam contoh tersebut, sisi kiri persamaan menunjukkan penjumlahan dari fungsi tangen (tan α) dan kotangen (cot α), sedangkan sisi kanan merupakan hasil dari perkalian fungsi sekannya (sec α) dan kosekannya (csc α). Meskipun kedua sisi ini awalnya terlihat berbeda dalam bentuk dan fungsi yang terlibat, mereka diakhiri dengan hasil yang sama, yang ditunjukkan oleh tanda “=”.
Adapun macam-macam rumus identitas trigonometri adalah sebagai berikut.
1. Rumus Identitas Trigonometri Ganjil Genap
- sin (-α) = -sin α
- cos (-α) = cos α
- tan (-α) = -tan α
2. Rumus Identitas Trigonometri Kofungsi
- sin (π/2 − α)= cos(α)
- cos (π/2 − α)= sin(α)
- tan (π/2 − α)= cot(α)
3. Rumus Identitas Trigonometri Pythagoras
- sin²(α) + cos² (α) = 1
- 1 + tan² (α) = sec²(α)
- 1 + cot² (α) = csc²(α)
4. Rumus Identitas Trigonometri Sudut Ganda
- sin(2α) = 2sin(α) cos(α)
- cos(2α)= cos²(α)−sin²(α) = 1 − 2sin²(α) = 2cos²(α) − 1
- tan(2α)= 2tan(α)/ 1 − tan²(α)
5. Rumus Identitas Trigonometri Setengah Sudut
- sin ½α = ± √(1 ‒ cos α)/2)
- cos ½α = ±√(1 + cos α)/2)
- tan ½α = ±√(1 ‒ cos α)/(1 + cos α) tan ½α = sin α/(1 + cos α) tan ½α = √(1 ‒ cos α)/ sin α
6. Rumus Identitas Trigonometri Jumlah dan Selisih Dua Sudut
- sin (α + β) = sin(α) cos(β) + cos(α) sin(β)
- sin (α − β) = sin(α) cos(β)− cos(α) sin(β)
- cos (α + β) = cos(α) cos(β) − sin(α) sin(β)
- cos (α − β) = cos(α) cos(β) + sin(α) sin(β)
- tan (α + β) = tan(α) + tan(β) / 1 − tan(α) tan(β)
- tan (α − β) = tan(α) − tan(β) / 1 + tan(α) tan(β)
7. Rumus Identitas Trigonometri Jumlah dan Selisih Fungsi Trigonometri Sinus dan Cosinus
- sin α + sin β = 2 sin ((α+β)/2) cos ((α-β)/2)
- sin α – sin β = 2 cos ((α+β)/2) sin ((α-β)/2)
- cos α + cos β = 2 cos ((α+β)/2) cos ((α-β)/2)
- cos α – cos β = -2 sin ((α+β)/2) sin ((α-β)/2)
8. Rumus Identitas Trigonometri Perkalian Fungsi Trigonometri Sinus dan Cosinus
- sin α sin β = -1/2 (cos(α+β) – cos(α-β))
- cos α cos β = 1/2 (cos(α+β) + cos(α-β))
- sin α cos β = 1/2 (sin(α+β) + sin(α-β))
- cos α sin β = 1/2 (sin(α+β) – sin(α-β))
Biar lebih mudah ngafalin dan mahaminnya, kamu bisa cek gambar rangkuman rumus identitas trigonometri berikut ini.

Sudut Istimewa
Pada beberapa segitiga, sulit untuk menentukan nilai pasti dari sisi-sisinya. Namun, ada jenis segitiga tertentu yang memiliki angka-angka yang presisi dan mudah dihitung. Segitiga ini disebut sudut istimewa.
Segitiga-segitiga ini disebut istimewa karena nilai sudut dan sisi mereka tepat dan pasti, sehingga sering digunakan dalam perhitungan trigonometri. Mereka juga dikenal sebagai sudut istimewa karena memiliki nilai-nilai yang sering muncul dan mudah diingat.
Kalau dilihat dari bentuknya, segitiga istimewa ini berasal dari bentuk-bentuk geometris yang sudah kita kenal dengan baik, seperti segitiga sama sisi dan persegi.
Segitiga sama sisi memiliki jumlah sudut total 180 derajat, dengan setiap sudutnya sebesar 60° derajat. Sedangkan persegi memiliki empat sudut yang masing-masing besarnya 90° derajat. Dari bentuk-bentuk dasar ini, kita dapat membangun segitiga-segitiga dengan sudut istimewa, seperti 30°, 45°, dan 60°.
Misalnya, jika kita membagi segitiga sama sisi menjadi dua bagian, kita mendapatkan segitiga dengan sudut 30°, 60°, dan 90°. Sedangkan dengan membagi persegi secara diagonal, kita mendapatkan segitiga dengan sudut 45°, 45°, dan 90°.
Nilai-nilai ini memiliki perbandingan sisi yang spesifik dan bisa dihitung menggunakan rumus trigonometri seperti sinus, kosinus, dan tangen. Berikut adalah tabel yang menunjukkan perbandingan sisi-sisi pada segitiga istimewa ini:
| α° | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin α° | 0 | 1/2 | 1/2 √2 | 1/2 √3 | 1 |
| cos α° | 1 | 1/2 √3 | 1/2 √2 | 1/2 | 0 |
| tan α° | 0 | 1/3 √3 | 1 | √3 | – |
| cot α° | – | √3 | 1 | 1/3 √3 | 0 |
| sec α° | 1 | 2/3 √3 | √2 | 2 | – |
| cosec α° | – | 2 | √2 | 2/3 √3 | 1 |
Dengan mengetahui sudut-sudut istimewa dan perbandingan sisi-sisinya, kita dapat dengan mudah menyelesaikan berbagai masalah trigonometri.
Penerapan Trigonometri Sehari-hari
Kamu sudah belajar pengertian dan berbagai macam rumus trigonometri. Sekarang, kamu harus tau betapa bermanfaatnya trigonometri di kehidupan manusia. Berikut ini adalah beberapa contoh aplikasi trigonometri dalam kehidupan sehari-hari.
1. Mengukur Ketinggian Pohon, Bangunan, atau Benda Lainnya
Trigonometri memungkinkan kita untuk menghitung ketinggian berbagai objek, seperti gunung, bukit, bangunan, dan pohon. Dengan menggunakan sudut elevasi, seseorang dapat mengukur ketinggian pohon tanpa harus memanjatnya.
Caranya adalah dengan mengukur sudut elevasi pandangan mata terhadap puncak pohon dan jarak dari titik pengamatan ke pohon tersebut. Metode yang sama seperti mengukur ketinggian pohon dapat digunakan untuk mengukur ketinggian gedung.
2. Mengatur Kemiringan Jalan atau Jembatan
Trigonometri memiliki peran yang sangat penting dalam rekayasa sipil untuk menentukan kemiringan jalan atau jembatan agar tetap aman bagi para pengguna. Perhitungan sudut dan kemiringan yang tepat mencegah risiko kecelakaan.
3. Membantu Tendangan Sepak Bola agar Lebih Tepat
Dalam olahraga seperti sepak bola, trigonometri membantu pemain mengatur sudut elevasi tendangan agar bola bisa masuk ke gawang lawan dengan presisi.
4. Bidang Navigasi
Dalam navigasi, perbandingan trigonometri digunakan untuk menghitung jarak suatu titik terhadap garis pantai. Ini penting bagi pelaut dan navigator untuk menentukan posisi kapal dengan tepat.
5. Bidang Oseanografi
Di bidang oseanografi, trigonometri digunakan untuk menghitung ketinggian gelombang laut. Ini membantu dalam memprediksi kondisi laut dan memberikan informasi penting bagi pelaut dan nelayan.
6. Bidang Astronomi
Trigonometri sangat berguna dalam astronomi. Karena ukuran benda-benda langit tidak dapat diukur langsung dengan alat pengukur biasa, astronom menggunakan skala-skala dan sudut-sudut untuk mengestimasi ukuran dan jarak benda langit dengan akurat.
7. Bidang Teknik Sipil
Pengukuran tanah adalah cabang ilmu alam yang menggunakan trigonometri untuk menentukan posisi tiga dimensi dari suatu tempat di permukaan bumi. Hasil pengukuran ini digunakan untuk membuat peta topografi dan menentukan luas wilayah suatu daerah.
8. Bidang Arsitektur
Trigonometri juga berperan penting dalam arsitektur. Ini digunakan untuk menentukan kemiringan atap, beban struktural, efek bayangan matahari, serta sudut cahaya terhadap bangunan, sehingga desain arsitektur menjadi lebih efisien dan estetis.
Contoh Soal & Pembahasan
Contoh Soal 1
Jennie menatap sebuah pohon yang berjarak 13 meter dari tempat ia berdiri. Tinggi Jennie adalah 168 cm. Jika sudut elevasi di tempat Jennie berdiri sebesar 50°, hitunglah tinggi pohon yang ada di hadapannya! (sin 50° = 0,7660; cos 50° = 0,6428; tan 50° = 1,1918).
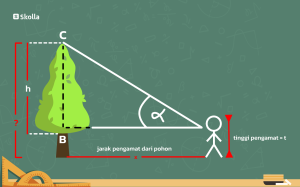
Pembahasan
Diketahui jarak Jennie dari pohon (x) adalah 13 meter. Tinggi Jennie (t) adalah 168 cm. Sudut elevasi di tempat Jennie berdiri (α) adalah 50°. Ditanya, berapa tinggi pohon?
Sehingga, jika tinggi pohon = tinggi Jennie + tinggi (h), maka
Tan α = h/x
Tan 50° = h/13 m
h = 13 m . tan 50°
h = 13 m . 1,1918
h = 15,4934 m
Lalu, tinggi pohon = tinggi Jennie + tinggi h
Tinggi pohon = 1,68 m + 15,4934 m
Tinggi pohon = 17,1734 m.
Jadi, tinggi pohon yang sedang dilihat oleh Jennie adalah 17,1734 meter.
Contoh Soal 2
Suprapto sedang bermain layangan. Dia kemudian berhasil menaikkan layang-layangnya hingga mencapai ketinggian 3,5 meter. Saat itu, dia memegang ujung pangkal benang layangan di ketinggian 60 cm dari permukaan tanah. Layangannya juga membentuk sudut ∠KIT sebesar 30°. Tentukan panjang tali layang-layang yang sudah diulurkan oleh Suprapto!
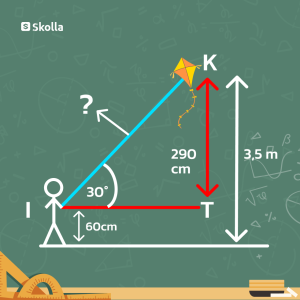
Pembahasan
Diketahui:
3,5 m = 350 cm.
Panjang KT (tinggi segitiga) 350-60 = 290 cm
Sin 30° = KT/KI
1/2 = 290 cm/KI
KI = 290 cm . 2
KI = 580 cm atau 5,8 m
Maka, panjang tali layang-layang yang sudah diulurkan oleh Suprapto adalah 580 cm atau 5,8 meter.
Contoh Soal 3
Terdapat sebuah segitiga siku-siku ABC. Huruf A mewakili sudut siku-sikunya. Maka, alas segitiga itu dapat disebut AB, tingginya AC, dan sisi miringnya BC. Diketahui bahwa nilai tan α° = 0,47. Jika panjang sisi AB = 12 cm, berapa panjang sisi AC?
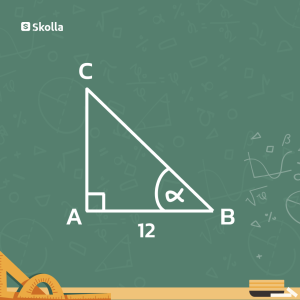
Pembahasan:
Diketahui tan α = 0,47. Ditanya, berapa panjang sisi depan (AC)?
Tan α = panjang sisi depan/panjang sisi samping
Tan α° = AC/AB
0,47 = AC/12 cm
AC = 0,47 x 12 cm = 5,64 cm.
Artinya panjang sisi AC adalah 5,64 cm.
Ingin menguasai Trigonometri lebih mendalam? Yuk, pelajari materinya lebih lanjut dan berlatih ribuan soal di aplikasi Skolla sekarang juga! Nikmati fleksibilitas belajar di mana saja dan kapan saja dengan ribuan konten pelajaran Matematika, Fisika, Kimia, Biologi, Bahasa Indonesia, hingga Bahasa Inggris hanya dalam satu langganan.
Jangan sampai ketinggalan, daftar sekarang untuk memulai perjalanan pendidikanmu yang seru dan informatif! Klik di sini untuk belajar Trigonometri di aplikasi Skolla.