Hai, Skollamate! Pernahkah kamu memperhatikan bentuk kaleng susu, gelas minum, atau pipa paralon di rumah? Kalau iya, berarti kamu sudah sering melihat bangun ruang ini dalam kehidupan sehari-hari!
Tabung adalah salah satu bangun ruang yang punya bentuk unik dan menarik. Bentuknya seperti drum atau gelas tinggi yang memiliki dua alas berbentuk lingkaran dan sisi melengkung yang membungkusnya.
Di artikel kali ini, kakmin akan menjelaskan tentang tabung, rumus, hingga contoh soalnya! Yuk, simak sampai akhir!
Pengertian Tabung dan Komponennya
Bayangkan sebuah lingkaran, lalu lingkaran itu diperpanjang ke atas hingga membentuk ruang, itulah tabung! Tabung termasuk bangun ruang karena memiliki volume alias bisa menampung sesuatu di dalamnya.
Dalam ilmu Matematika, tabung adalah bangun ruang tiga dimensi yang memiliki dua alas berbentuk lingkaran yang identik dan sebuah selimut berbentuk persegi panjang yang melingkar menghubungkan kedua alasnya.
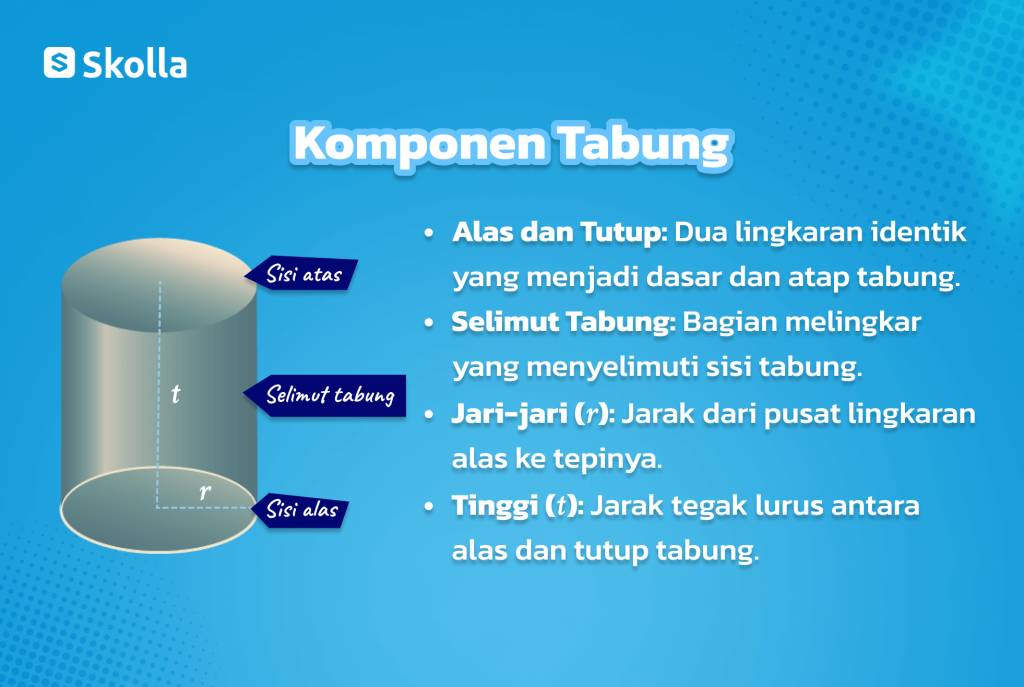
Beberapa komponen utama tabung meliputi:
- Alas dan Tutup: Dua lingkaran identik yang menjadi dasar dan atap tabung.
- Selimut Tabung: Bagian melingkar yang menyelimuti sisi tabung.
- Jari-jari (r): Jarak dari pusat lingkaran alas ke tepinya.
- Tinggi (t): Jarak tegak lurus antara alas dan tutup tabung.
Bentuknya unik, kan? Supaya lebih paham, yuk kenalan lebih jauh dengan bagian-bagian tabung berikut ini!
Rumus Tabung
Karena bentuknya yang khas, tabung punya rumus khusus untuk menghitung volume (isi) dan luas permukaannya. Jangan khawatir, Kakmin bakal jelasin semuanya dengan cara yang seru dan mudah dipahami! 😆
Rumus Volume Tabung
Volume tabung dihitung dengan mengalikan luas alas dengan tinggi tabung.
V = π × r² × t
Keterangan:
- V = volume tabung
- r = jari-jari alas tabung
- t = tinggi tabung
- π = 3,14 atau 22/7 (tergantung soal)
Rumus Luas Permukaan Tabung
Luas permukaan tabung terdiri dari luas dua lingkaran (alas dan tutup) serta luas selimut tabung.
L = 2 × π × r² + 2 × π × r × t
Keterangan:
- L = luas permukaan tabung
- π = 3,14 atau 22/7 (tergantung soal)
- r = jari-jari alas tabung
- t = tinggi tabung
- 2 × π × r² = luas dua alas tabung
- 2 × π × r × t = luas dua selimut tabung
Rumus Luas Permukaan Tabung Tanpa Tutup
Jika tabung tidak memiliki tutup, luas permukaannya hanya terdiri dari satu alas dan selimut tabung.
L = π × r² + 2 × π × r × t
Keterangan:
- L = luas permukaan tabung
- π = 3,14 atau 22/7 (tergantung soal)
- r = jari-jari alas tabung
- t = tinggi tabung
- π × r² = luas satu alas tabung
- π × r × t = luas satu selimut tabung
Rumus Luas Selimut Tabung
Selimut tabung berbentuk persegi panjang dengan panjang keliling alas dan tinggi sebagai lebarnya.
L_selimut = 2 × π × r × t
Keterangan:
- L = luas selimut tabung
- π = 3,14 atau 22/7 (tergantung soal)
- r = jari-jari alas tabung
- t = tinggi tabung

Contoh Soal dan Pembahasan
1. Tentukan volume tabung jika diketahui jari-jari 14 cm dan tinggi 30 cm!
Diketahui:
- r = 14 cm
- t = 30 cm
- π = 22/7
Ditanya: Berapa volume tabung?
Jawaban:
Gunakan rumus volume tabung:
V = π × r² × t
V = (22/7) × (14 × 14) × 30
V = (22/7) × 196 × 30
V = 22 × 28 × 30
V = 18.480 cm³
Jadi, volume tabung adalah 18.480 cm³.
2. Tentukan tinggi tabung jika diketahui volume 6.280 cm³ dan jari-jari 10 cm!
Diketahui:
- V = 6.280 cm³
- r = 10 cm
- π = 3,14
Ditanya: Berapa tinggi tabung?
Jawaban:
Gunakan rumus volume tabung:
V = π × r² × t
6.280 = 3,14 × (10 × 10) × t
6.280 = 3,14 × 100 × t
6.280 = 314 × t
t = 6.280 ÷ 314
t = 20 cm
Jadi, tinggi tabung adalah 20 cm.
3. Tentukan jari-jari tabung jika diketahui volume 2.826 cm³ dan tinggi 9 cm!
Diketahui:
- V = 2.826 cm³
- t = 9 cm
- π = 3,14
Ditanya: Berapa jari-jari tabung?
Jawaban:
Gunakan rumus volume tabung:
V = π × r² × t
2.826 = 3,14 × r² × 9
2.826 = 28,26 × r²
r² = 2.826 ÷ 28,26
r² = 100
r = √100
r = 10 cm
Jadi, jari-jari tabung adalah 10 cm.
4. Tentukan volume tabung jika diketahui diameter 20 cm dan tinggi 15 cm!
Diketahui:
- Diameter (d) = 20 cm sehingga jari-jari (r) = d ÷ 2 = 10 cm
- t = 15 cm
- π = 3,14
Ditanya: Berapa volume tabung?
Jawaban:
Gunakan rumus volume tabung:
V = π × r² × t
V = 3,14 × (10 × 10) × 15
V = 3,14 × 100 × 15
V = 4.710 cm³
Jadi, volume tabung adalah 4.710 cm³.
5. Tentukan luas permukaan tabung jika diketahui jari-jari 7 cm dan tinggi 12 cm!
Diketahui:
- r = 7 cm
- t = 12 cm
- π = 22/7
Ditanya: Berapa luas permukaan tabung?
Jawaban:
Gunakan rumus luas permukaan tabung:
L = 2 × π × r² + 2 × π × r × t
L = 2 × (22/7) × (7 × 7) + 2 × (22/7) × 7 × 12
L = 2 × (22/7) × 49 + 2 × (22/7) × 84
L = 2 × 154 + 2 × 264
L = 308 + 528
L = 836 cm²
Jadi, luas permukaan tabung adalah 836 cm².
6. Tentukan luas permukaan tabung tanpa tutup jika diketahui diameter 14 cm dan tinggi 20 cm!
Diketahui:
- Diameter (d) = 14 cm sehingga jari-jari (r) = 14 ÷ 2 = 7 cm
- t = 20 cm
- π = 3,14
Ditanya: Berapa luas permukaan tabung tanpa tutup?
Jawaban:
Gunakan rumus luas permukaan tabung tanpa tutup:
L = π × r² + 2 × π × r × t
L = 3,14 × (7 × 7) + 2 × 3,14 × 7 × 20
L = 3,14 × 49 + 2 × 3,14 × 140
L = 153,86 + 879,2
L = 1.033,06 cm²
Jadi, luas permukaan tabung tanpa tutup adalah 1.033,06 cm².
7. Tentukan luas permukaan tabung dan tinggi jika diketahui luas selimut 528 cm² dan jari-jari 7 cm!
Diketahui:
- L_selimut = 528 cm²
- r = 7 cm
- π = 22/7
Ditanya: Berapa luas permukaan tabung dan tinggi tabung?
Jawaban:
Gunakan rumus luas selimut tabung:
L_selimut = 2 × π × r × t
528 = 2 × (22/7) × 7 × t
528 = 44 × t
t = 528 ÷ 44
t = 12 cm
Sekarang hitung luas permukaan tabung:
L = 2 × π × r² + 2 × π × r × t
L = 2 × (22/7) × (7 × 7) + 528
L = 2 × 154 + 528
L = 308 + 528
L = 836 cm²
Jadi, luas permukaan tabung adalah 836 cm² dan tingginya 12 cm.
8. Tentukan luas selimut tabung jika diketahui jari-jari 5 cm dan tinggi 18 cm!
Diketahui:
- r = 5 cm
- t = 18 cm
- π = 3,14
Ditanya: Berapa luas selimut tabung?
Jawaban:
Gunakan rumus luas selimut tabung:
L_selimut = 2 × π × r × t
L_selimut = 2 × 3,14 × 5 × 18
L_selimut = 2 × 3,14 × 90
L_selimut = 565,2 cm²
Jadi, luas selimut tabung adalah 565,2 cm².
Baca Juga: Rumus Lingkaran: Keliling, Luas, Jari-Jari, Diameter, dan Contoh Soal
Nah, Skollamate, sekarang kamu sudah tahu banyak tentang tabung, mulai dari pengertiannya, rumus luas permukaan, volume, hingga contoh soal yang bisa bikin kamu makin paham. Seru, kan? 😆
Tapi ingat, ini baru satu dari banyak bangun ruang yang ada di Matematika. Masih ada prisma, limas, dan kerucut yang juga penting untuk dipelajari. Jangan khawatir! Semua materi lengkap tentang bangun ruang bisa kamu temukan di aplikasi Skolla, lho!
Di Skolla, kamu bisa belajar bangun ruang di video belajar interaktif, live class seru, dan ribuan latihan soal yang siap mengasah kemampuan Matematikamu. Semakin sering latihan, semakin jago kamu dalam memahami konsep bangun ruang! Jadi, tunggu apa lagi? Yuk, belajar di Skolla sekarang juga ya!